The divide-and-conquer paradigm is often used to find an optimal solution to a problem. Its basic idea is to decompose a given problem into two or more similar, but simpler, subproblems, to solve them in turn, and to compose their solutions to solve the given problem. Problems of sufficient simplicity are solved directly. For example, to sort a given list of n natural numbers, split it into two lists of about n/2 numbers each, sort each of them in turn, and interleave both results appropriately to obtain the sorted version of the given list (see the picture). This approach is known as the merge sort algorithm.

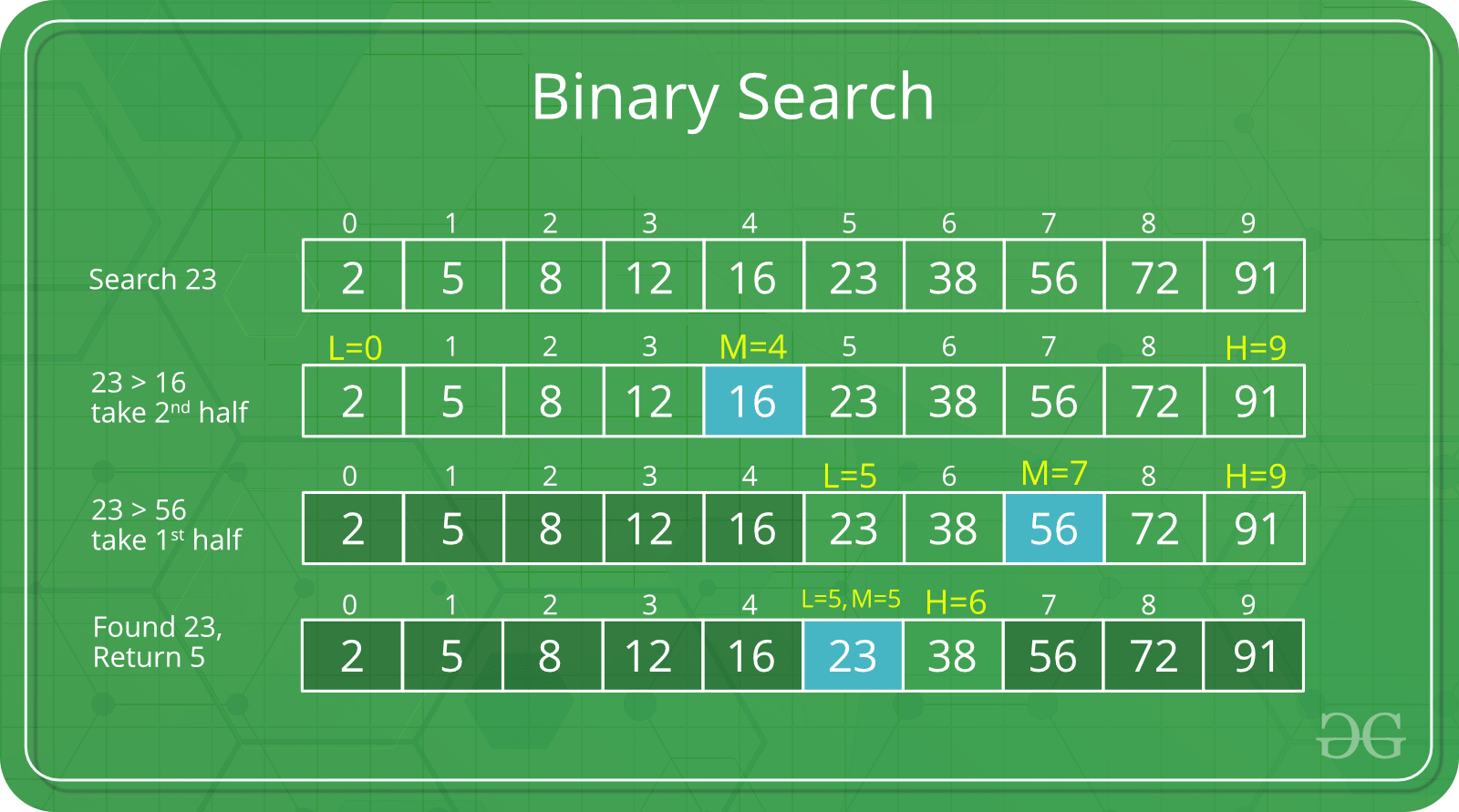
The name "divide and conquer" is sometimes applied to algorithms that reduce each problem to only one sub-problem, such as the binary search algorithm for finding a record in a sorted list (or its analog in numerical computing, the bisection algorithm for root finding). These algorithms can be implemented more efficiently than general divide-and-conquer algorithms; in particular, if they use tail recursion, they can be converted into simple loops. Under this broad definition, however, every algorithm that uses recursion or loops could be regarded as a "divide-and-conquer algorithm". Therefore, some authors consider that the name "divide and conquer" should be used only when each problem may generate two or more subproblems. The name decrease and conquer has been proposed instead for the single-subproblem class.

As an example of a divide-and-conquer algorithm that did not originally involve computers, Donald Knuth gives the method a post office typically uses to route mail: letters are sorted into separate bags for different geographical areas, each of these bags is itself sorted into batches for smaller sub-regions, and so on until they are delivered. This is related to a radix sort, described for punch-card sorting machines as early as 1929.

Source: https://en.wikipedia.org/wiki/Divide-and-conquer_algorithm

              Donald E. Knuth, The Art of Computer Programming: Volume 3, Sorting and Searching, second edition                    (Addison-Wesley, 1998).